通信人家园

标题: 软判决译码和硬判决译码 [查看完整版帖子] [打印本页]

时间: 2021-2-2 10:20

作者: 7896324 标题: 软判决译码和硬判决译码

一、卷积编码仿真（硬判决译码误码率和理论值比较）
已知卷积码生成函数：

可知码率为1/3，相应的抽头系数为（557 663 711）的卷积码。编写程序，采用卷积编码、维特比译码（硬判决），BPSK调制解调，高斯白噪声的条件，仿真得到误码率随着信道信噪比变化的关系，结果如下图所示：

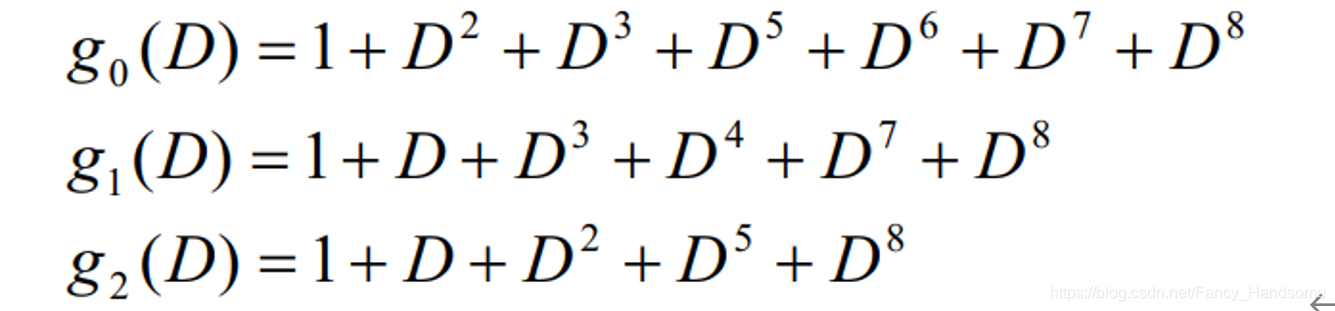
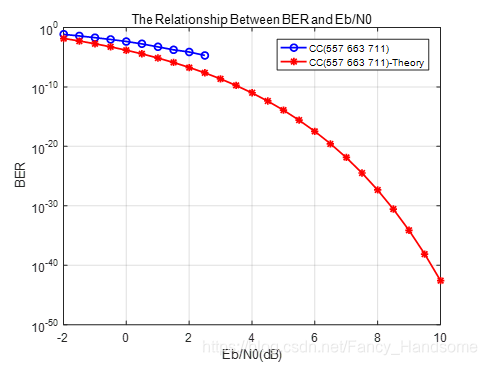
红色曲线为理论值，蓝色曲线为实际值。可以看到，实际的误码率值略高于理论的误码率值，这一点符合实际。这表明需要对解码算法进行改进提升，使误码率进一步逼近理论值。

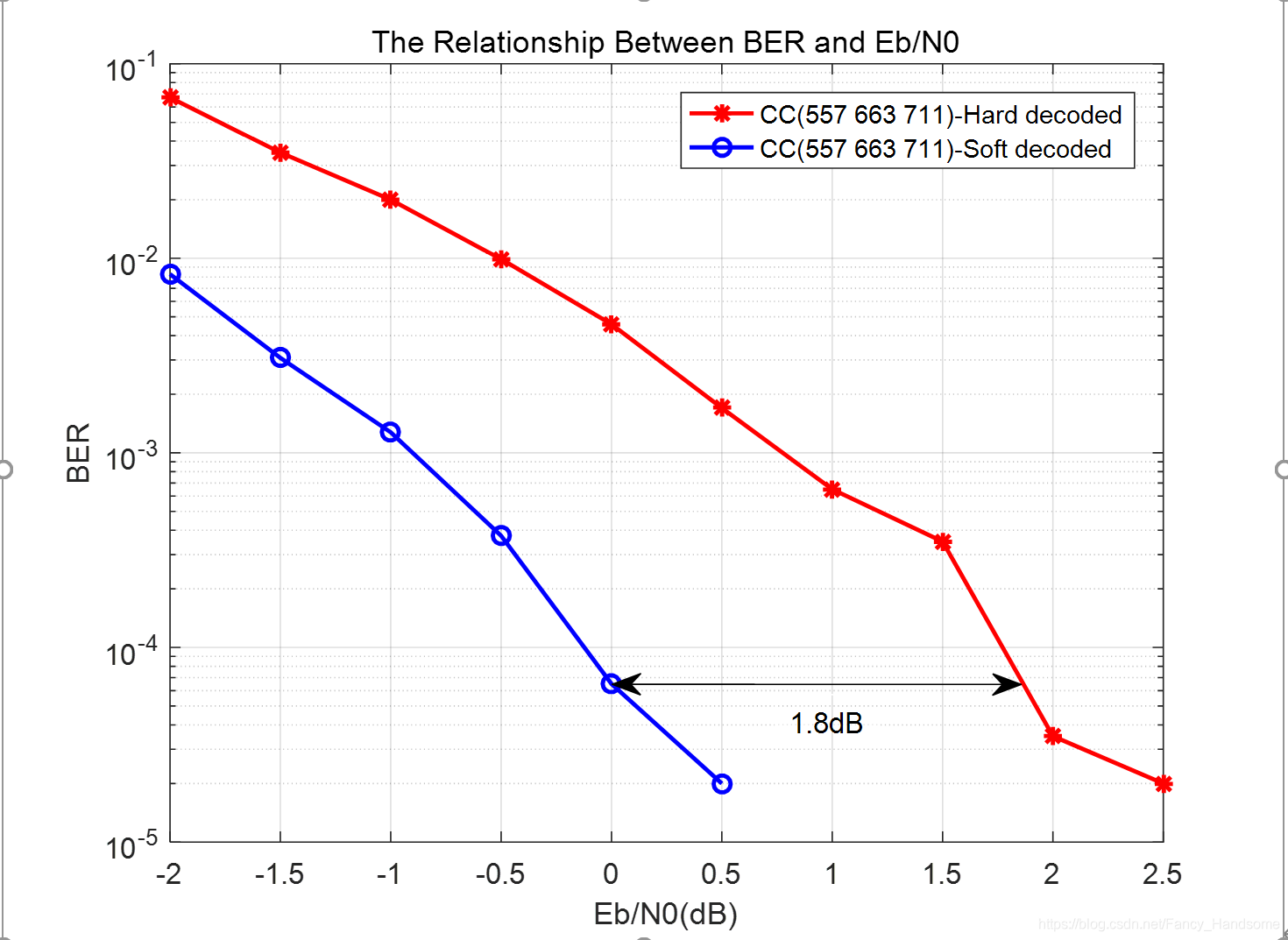
二、卷积编码软硬判决误码率比较
在第一步的基础上，相同条件，采用软判决规则，对比误码率提升，结果如下：

红色曲线为基于硬判决的误码率仿真曲线。蓝色曲线为基于软判决的误码率仿真曲线。从图中可以看出，软判决比硬判决，在性能上有1.8dB（接近2dB）的提升，与理论相符。

三、相关代码

####卷积编码程序

clc;

close all;

clear all;

%% 初始参数设定

EbN0=-2:0.5:10;%信噪比范围设定

L=200000;%设定码元个数

data=randi([0,1],1,L);%信息码元生成

A = 5; %卷积码生成函数的最高次项系数

bf = 18;

%% 信道编码

len = 9; % 约束长度，一共到D8，相当于有9个寄存器

treliss=poly2trellis(len,[557 663 711]);%抽头系数(101101111,110110011,111001001)

encode= convenc(data,treliss);% 信道编码

%% 信道加噪声计算

j=1;

for S0=-2:0.5:10%开始试验

% 计算理论上误码率值

Pe=0.5*erfc((10^(0.1*S0))^0.5);

Error_Bit_Theory(j)=A*2^bf*Pe^(bf/2);

% 信息序列调制-加噪声-解调

[codes_bsc,codes]=BPSK_AddNoise(encode,S0);

% 硬判决译码

decoded1 = vitdec(codes_bsc,treliss,len,'trunc','hard');

Error_Bit_Hard(j)=1-length(find(data==decoded1))/L; %误码率统计

%软判决译码

[x,qcode]=quantiz(-codes,[-0.875 -0.75,-0.625 -0.5,-0.375 -0.25,-0.125 0,0.125 0.25,0.375 0.5,0.625 0.75 0.875],15:-1:0);%截获码元软判决量化

decoded2=vitdec(qcode,treliss,len,'trunc','soft',4);

Error_Bit_Soft(j)=1-length(find(data==decoded2))/L;%误码率统计

j=j+1;

end

%% 画图对比性能提升

figure

semilogy(EbN0,Error_Bit_Hard,'-ob','linewidth',1.5);hold on;

semilogy(EbN0,Error_Bit_Theory,'-*r','linewidth',1.5);

legend('CC(557 663 711)','CC(557 663 711)-Theory');

grid on;

ylabel('BER');

xlabel('Eb/N0(dB)');

title('The Relationship Between BER and Eb/N0');

figure

semilogy(EbN0,Error_Bit_Hard,'-*r','linewidth',1.5);hold on

semilogy(EbN0,Error_Bit_Soft,'-ob','linewidth',1.5);

legend('CC(557 663 711)-Hard decoded','CC(557 663 711)-Soft decoded');

grid on;

ylabel('BER');

xlabel('Eb/N0(dB)');

title('The Relationship Between BER and Eb/N0');

###信道加噪声程序
function [Msg_BSC,Msg]=BPSK_AddNoise(msg,snr)
% 调制
msg1=2*msg-1; %星座映射0映射为-1,1映射为1

% 加噪声
sigma=(1/(2*(10^(0.1*snr))));
noise=0+(sigma)^0.5.*randn(1,length(msg)); %加高斯白噪声，sigma为信噪比方差
Msg=msg1+noise; %加噪声后的信息序列

% 解调，加噪声以后，需要信息序列恢复成0-1比特序列
for i=1:length(msg);
if Msg(i)>0
Msg_BSC(i)=1;
else
Msg_BSC(i)=0;
end
end
end

通信人家园 (https://www.txrjy.com/)